DAGs and potential outcomes

# DAGs and potential outcomes

**Session 5**

]

---

# Plan for today

.box-5.medium.sp-after-half[*do*()ing observational causal inference]

.box-7.medium[Potential outcomes]

---

name: dag-adjustment
class: center middle section-title section-title-5 animated fadeIn

# *do*()ing observational causal inference

---

---

# Structural models

.box-inv-5.small[The relationship between nodes can be described with equations]

$$
`\begin{aligned}
\text{Loc} &= f_\text{Loc}(\text{U1}) \\
\text{Bkgd} &= f_\text{Bkgd}(\text{U1}) \\
\text{JobCx} &= f_\text{JobCx}(\text{Edu}) \\
\text{Edu} &= f_\text{Edu}(\text{Req}, \text{Loc}, \text{Year}) \\
\text{Earn} &= f_\text{Earn}(\text{Edu}, \text{Year}, \text{Bkgd}, \\
& \quad\quad\quad\quad \text{Loc}, \text{JobCx}) \\
\end{aligned}`
$$
]

.pull-right[
<img src="05-slides_files/figure-html/structural-dag-1.png" width="90%" style="display: block; margin: auto;" />
]
---

# Structural models

.pull-left.small[
$$
`\begin{aligned}
\text{Earn} &= f_\text{Earn}(\text{Edu}, \text{Year}, \text{Bkgd}, \\
& \quad\quad\quad\quad \text{Loc}, \text{JobCx}) \\
\text{Edu} &= f_\text{Edu}(\text{Req}, \text{Loc}, \text{Year}) \\
\text{JobCx} &= f_\text{JobCx}(\text{Edu}) \\
\text{Bkgd} &= f_\text{Bkgd}(\text{U1}) \\
\text{Loc} &= f_\text{Loc}(\text{U1})
\end{aligned}`
$$
]

.pull-right.small-code[

```r
dagify(
  Earn ~ Edu + Year + Bkgd + Loc + JobCx,
  Edu ~ Req + Loc + Bkgd + Year,
  JobCx ~ Edu,
  Bkgd ~ U1,
  Loc ~ U1
)
```

]

---

# Causal identification

]

]

---

# Causal identification

.box-inv-5.medium[A causal effect is *identified* if the association between treatment and outcome is propertly stripped and isolated]

---

# Paths and associations

.box-inv-5.medium[Arrows in a DAG transmit associations]

.box-inv-5.medium[You can redirect and control those paths by "adjusting" or "conditioning"]

---

# Three types of associations

.box-inv-5.small[Common cause]
]

.pull-middle-3.center[
.box-5.medium[Causation]

.box-inv-5.small[Mediation]
]

.box-inv-5.small[Selection / endogeneity]
]

---

# Interventions

.box-inv-5.medium[*do*-operator]

$$
P[Y\ |\ do(X = x)] \quad \text{or} \quad E[Y\ |\ do(X = x)]
$$

---

# Interventions

$$
E[Y\ |\ do(X = x)]
$$

---

# Interventions

.pull-left[
.box-5.small[Observational DAG]
<img src="05-slides_files/figure-html/observational-dag-1.png" width="90%" style="display: block; margin: auto;" />
]

.pull-right[
.box-5.small[Experimental DAG]
<img src="05-slides_files/figure-html/experimental-dag-1.png" width="90%" style="display: block; margin: auto;" />
]

---

# Interventions

$$
E[\text{Earnings}\ |\ do(\text{College education})]
$$

]

<img src="05-slides_files/figure-html/edu-earn-experiment-1.png" width="90%" style="display: block; margin: auto;" />
]

---

# Un*do*()ing things

.box-inv-5.medium[We want to know **P[Y | *do*(X)]** but all we have is observational data X, Y, and Z]

$$
P[Y\ |\ do(X)] \neq P(Y\ |\ X)
$$

---

# Un*do*()ing things

.box-inv-5.medium[Our goal with observational data: Rewrite **P[Y | *do*(X)]** so that it doesn't have a *do*() anymore (is "*do*-free")]

---

# *do*-calculus

.box-inv-5[A set of three rules that let you manipulate a DAG in special ways to remove *do*() expressions]

.center[
<figure>
 <img src="img/05/do-calculus.png" alt="do-calculus rules" title="do-calculus rules" width="40%">
</figure>
]

.box-5.smaller[WAAAAAY beyond the score of this class! Just know it exists and computer algorithms can do it for you!]

???

https://arxiv.org/abs/1906.07125

---

# Special cases of *do*-calculus

.box-inv-5.medium.sp-after[Backdoor adjustment]

.box-inv-5.medium[Frontdoor adjustment]

---

# Backdoor adjustment

$$
P[Y\ |\ do(X)] = \sum_Z P(Y\ |\ X, Z) \times P(Z)
$$

.pull-left[
<img src="05-slides_files/figure-html/backdoor-dag-1.png" width="90%" style="display: block; margin: auto;" />
]

---

# Frontdoor adjustment

.box-5.small[**S → T** is *d*-separated; **T → C** is *d*-separated combine the effects to find **S → C**]

---

# Moral of the story

.box-inv-5.medium[If you can transform *do*() expressions to *do*-free versions, you can legally make causal inferences from observational data]

.box-5.small[Fancy algorithms (found in the **causaleffect** package) can do the official *do*-calculus for you too]

---

layout: false
name: potential-outcomes
class: center middle section-title section-title-7 animated fadeIn

# Potential outcomes

---

---

# Program effect

---

# Some equation translations

.box-inv-7.medium[Causal effect = δ (delta)]

$$
\delta = P[Y\ |\ do(X)]
$$

$$
\delta = E[Y\ |\ do(X)] - E[Y\ |\ \hat{do}(X)]
$$

$$
\delta = (Y\ |\ X = 1) - (Y\ |\ X = 0)
$$

$$
\delta = Y_1 - Y_0
$$

---

???

https://www.thisamericanlife.org/691/gardens-of-branching-paths

---

---

.box-7.large[Fundamental problem of causal inference]

$$
\delta_i = Y_i^1 - Y_i^0 \quad \text{in real life is} \quad \delta_i = Y_i^1 - ???
$$

---

---

# Average treatment effect (ATE)

.box-inv-7.medium[Solution: Use averages instead]

$$
\text{ATE} = E(Y_1 - Y_0) = E(Y_1) - E(Y_0)
$$

.box-7[Difference between average/expected value when program is on vs. expected value when program is off]

$$
\delta = (\bar{Y}\ |\ P = 1) - (\bar{Y}\ |\ P = 0)
$$

---

| Person | Age | Treated | Outcome with program | Outcome without program | Effect |
|:------:|:-----:|:-------:|:-----------------------:|:--------------------------:|:-------:|
| 1 | Old | TRUE | **80** | 60 | **20** |
| 2 | Old | TRUE | **75** | 70 | **5** |
| 3 | Old | TRUE | **85** | 80 | **5** |
| 4 | Old | FALSE | 70 | **60** | **10** |
| 5 | Young | TRUE | **75** | 70 | **5** |
| 6 | Young | FALSE | 80 | **80** | **0** |
| 7 | Young | FALSE | 90 | **100** | **-10** |
| 8 | Young | FALSE | 85 | **80** | **5** |
]

---

.smaller.sp-after[

.pull-left.small[
`$\delta = (\bar{Y}\ |\ P = 1) - (\bar{Y}\ |\ P = 0)$`
]

.pull-right.small[
`$\text{ATE} = \frac{20 + 5 + 5 + 5 + 10 + 0 + -10 + 5}{8} = 5$`
]

---

# CATE

.box-inv-7.sp-after[ATE in subgroups]

.box-7.medium[Is the program more effective for specific age groups?]

---

.smaller.sp-after[

.pull-left.small[
`$\delta = (\bar{Y}_\text{O}\ |\ P = 1) - (\bar{Y}_\text{O}\ |\ P = 0)$`

`$\delta = (\bar{Y}_\text{Y}\ |\ P = 1) - (\bar{Y}_\text{Y}\ |\ P = 0)$`
]

.pull-right.small[
`$\text{CATE}_\text{Old} = \frac{20 + 5 + 5 + 10}{4} = 10$`

`$\text{CATE}_\text{Young} = \frac{5 + 0 - 10 + 5}{4} = 0$`
]

---

# ATT and ATU

.box-inv-7.medium[Average treatment on the treated]

.box-inv-7.medium[Average treatment on the untreated]

---

.smaller.sp-after[

.pull-left.small[
`$\delta = (\bar{Y}_\text{T}\ |\ P = 1) - (\bar{Y}_\text{T}\ |\ P = 0)$`

`$\delta = (\bar{Y}_\text{U}\ |\ P = 1) - (\bar{Y}_\text{U}\ |\ P = 0)$`
]

.pull-right.small[
`$\text{CATE}_\text{Treated} = \frac{20 + 5 + 5 + 5}{4} = 8.75$`

`$\text{CATE}_\text{Untreated} = \frac{10 + 0 - 10 + 5}{4} = 1.25$`
]

---

---

# ATE, ATT, and ATU

.box-inv-7.medium.sp-after[The ATE is the weighted average of the ATT and ATU]

.center[
`$\text{ATE} = (\pi_\text{Treated} \times \text{ATT}) + (\pi_\text{Untreated} \times \text{ATU})$`

`$(\frac{4}{8} \times 8.75) + (\frac{4}{8} \times 1.25)$`

`$4.375 + 0.625 = 5$`
]

.box-7.smaller[**π** here means "proportion," not 3.1415]

---

# Selection bias

.box-inv-7.medium[ATE and ATT aren't always the same]

.box-inv-7.medium[ATE = ATT + Selection bias]

$$
`\begin{aligned}
5 &= 8.75 + x \\
x &= -3.75
\end{aligned}`
$$

---

# Actual data

.pull-left.smaller[

| Person |  Age  | Treated | Actual outcome |
|:------:|:-----:|:-------:|:--------------:|
|   1    |  Old  |  TRUE   |       80       |
|   2    |  Old  |  TRUE   |       75       |
|   3    |  Old  |  TRUE   |       85       |
|   4    |  Old  |  FALSE  |       60       |
|   5    | Young |  TRUE   |       75       |
|   6    | Young |  FALSE  |       80       |
|   7    | Young |  FALSE  |      100       |
|   8    | Young |  FALSE  |       80       |
]

---

# Actual data

.pull-left.smaller[

<img src="05-slides_files/figure-html/po-dag-1.png" width="100%" style="display: block; margin: auto;" />
]

---

# Actual data

.pull-left.tiny[

.box-inv-7.tiny[As long as we assume/pretend treatment was randomly assigned within each age = unconfoundedness]

]

&nbsp;

.center[
`$\widehat{\text{ATE}} = \pi_\text{Old} \widehat{\text{CATE}_\text{Old}} + \pi_\text{Young} \widehat{\text{CATE}_\text{Young}}$`
]

---

# Actual data

.center.sp-after[
`$\color{#FF851B}{\widehat{\text{ATE}}} = \pi_\text{Old} \color{#2ECC40}{\widehat{\text{CATE}_\text{Old}}} + \pi_\text{Young} \color{#0074D9}{\widehat{\text{CATE}_\text{Young}}}$`
]

.pull-left-narrow.tiny[

.pull-right-wide.small[
&nbsp;

`$\color{#2ECC40}{\widehat{\text{CATE}_\text{Old}}} = \frac{80 + 75 + 85}{3} - \frac{60}{1} = \color{#2ECC40}{20}$`

`$\color{#0074D9}{\widehat{\text{CATE}_\text{Young}}} = \frac{75}{1} - \frac{80 + 100 + 80}{3} = \color{#0074D9}{-11.667}$`

`$\color{#FF851B}{\widehat{\text{ATE}}} = (\frac{4}{8} \times \color{#2ECC40}{20}) + (\frac{4}{8} \times \color{#0074D9}{-11.667}) = \color{#FF851B}{4.1667}$`
]

---

# ¡¡¡DON'T DO THIS!!!

.center.sp-after[
`$\color{#FF851B}{\widehat{\text{ATE}}} = \color{#F012BE}{\widehat{\text{CATE}_\text{Treated}}} - \color{#AAAAAA}{\widehat{\text{CATE}_\text{Untreated}}}$`
]

.pull-left-narrow.tiny[

.pull-right-wide.small.center[
`$\color{#F012BE}{\widehat{\text{CATE}_\text{Treated}}} = \frac{80 + 75 + 85 + 75}{4} = \color{#F012BE}{78.75}$`

`$\color{#AAAAAA}{\widehat{\text{CATE}_\text{Untreated}}} = \frac{60 + 80 + 100 + 80}{4} = \color{#AAAAAA}{80}$`

`$\color{#FF851B}{\widehat{\text{ATE}}} = \color{#F012BE}{78.75} - \color{#AAAAAA}{80} = \color{#FF851B}{-1.25}$`

&nbsp;

---

# Matching and ATEs

.center[
`$\widehat{\text{ATE}} = \pi_\text{Old} \widehat{\text{CATE}_\text{Old}} + \pi_\text{Young} \widehat{\text{CATE}_\text{Young}}$`
]

.box-7.small[And we assumed unconfoundedness; that treatment is randomly assigned within the groups]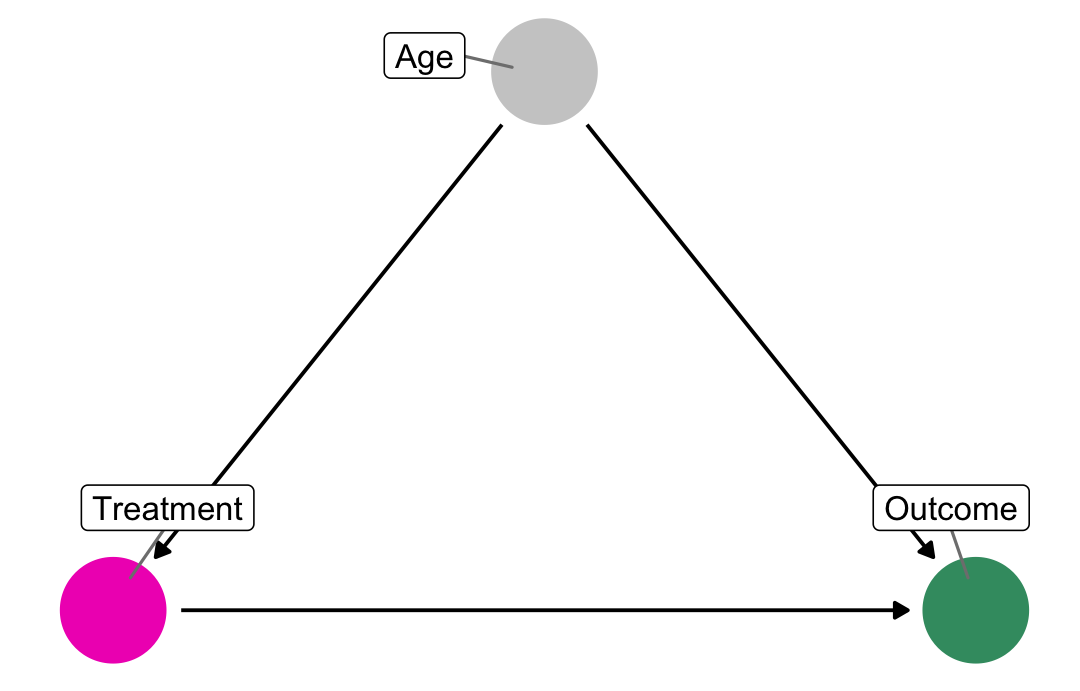
]

---

&nbsp;

.pull-right-wide[
<figure>
 <img src="img/05/mm-matching.png" alt="Matching table from Mastering 'Metrics" title="Matching table from Mastering 'Metrics" width="100%">
</figure>
]

---

.pull-left-wide[
<figure>
 <img src="img/05/mm-matching.png" alt="Matching table from Mastering 'Metrics" title="Matching table from Mastering 'Metrics" width="90%">
</figure>
]

.tiny[
$$
`\begin{aligned}
\frac{110 + 100 + 60 + 115 + 75}{5} &= \color{#0074D9}{92} \\
\frac{110 + 30 + 90 + 60}{4} &= \color{#2ECC40}{72.5} \\
(\color{#0074D9}{92} \times \color{#7FDBFF}{\frac{5}{9}}) - (\color{#2ECC40}{72.5} \times \color{#01FF70}{\frac{4}{9}}) &= \color{#FF851B}{18,888}
\end{aligned}`
$$
]

.center[
`$\color{#FF851B}{\widehat{\text{ATE}}} = \color{#7FDBFF}{\pi_\text{Private}} \color{#0074D9}{\widehat{\text{CATE}_\text{Private}}} + \color{#01FF70}{\pi_\text{Public}} \color{#2ECC40}{\widehat{\text{CATE}_\text{Public}}}$`
]

---

# Grouping and matching

.pull-left[
<figure>
 <img src="img/05/mm-matching.png" alt="Matching table from Mastering 'Metrics" title="Matching table from Mastering 'Metrics" width="100%">
</figure>
]

.box-inv-7.tiny[Unconfoundedness?]

<img src="05-slides_files/figure-html/match-dag-1.png" width="80%" style="display: block; margin: auto;" />
]

---

.pull-left-wide[
<figure>
 <img src="img/05/mm-matching.png" alt="Matching table from Mastering 'Metrics" title="Matching table from Mastering 'Metrics" width="90%">
</figure>
]

.tiny[
$$
`\begin{aligned}
\frac{110 + 100}{2} - 110 &= \color{#0074D9}{-5,000} \\
60 - 30 &= \color{#2ECC40}{30,000} \\
(\color{#0074D9}{-5} \times \color{#7FDBFF}{\frac{3}{5}}) + (\color{#2ECC40}{30} \times \color{#01FF70}{\frac{2}{5}}) &= \color{#FF851B}{9,000}
\end{aligned}`
$$
]

.center[
`$\color{#FF851B}{\widehat{\text{ATE}}} = \color{#7FDBFF}{\pi_\text{Group A}} \color{#0074D9}{\widehat{\text{CATE}_\text{Group A}}} + \color{#01FF70}{\pi_\text{Group B}} \color{#2ECC40}{\widehat{\text{CATE}_\text{Group B}}}$`
]

---

# Matching with regression

$$
\text{Earnings} = \alpha + \beta_1 \text{Private} + \beta_2 \text{Group} + \epsilon
$$

.small-code.center[

```r
model_earnings <- lm(earnings ~ private + group_A, data = schools_small)
```
]

|term        | estimate| std.error| statistic| p.value|
|:-----------|--------:|---------:|---------:|-------:|
|(Intercept) |    40000|  11952.29|      3.35|    0.08|
|privateTRUE |    10000|  13093.07|      0.76|    0.52|
|group_ATRUE |    60000|  13093.07|      4.58|    0.04|
]

.center.float-left[
.box-7[β1 = $10,000]&emsp;.box-7[This is less wrong!]&emsp;.box-7[Significance details!]
]